物理经济学：从黑洞理论、热力学等理论中看清

当理论学家们在讨论毕苏期权定价模式神奇之处时，华尔街交易员已经用它来赚钱。这促使我们更深入地探究不同科学与经济学领域之间的相互联系。首先，当我们发现这样一个被称为物理经济学的领域的存在时，我们非常惊讶，它把理论物理学，量子力学和其他一些物理学分支的知识运用到经济学中。

这篇文章主要讨论了三种类型的领域，在这些领域中，物理学家建立的模型已经被用来发展一种新的视角来看待经济学。

布朗运动：物理学、生物学和经济学结合在一起的概念

你是否见过并想知道悬浮在流体中的小颗粒是如何运动的？

二维布朗运动

布朗运动的发现通常被认为是苏格兰植物学家罗伯特·布朗的功劳。他在显微镜下观察了悬浮在水中的花粉粒的随机运动。在发现布朗之后的大约80年，理论物理学家阿尔伯特·爱因斯坦发表了一篇论文，他模拟了花粉颗粒被单个水分子扰动而运动的过程，这是他最初的主要科学贡献之一。但一个鲜为人知的事实是，在爱因斯坦发表论文的5年前，一位名叫路易斯?巴切利耶的年轻法国数学家，在金融市场资产价格的背景下，描述了一个与爱因斯坦描述的布朗运动非常相似的现象。50多年后，在1956年巴切利耶的论文引起了著名经济学家、诺贝尔奖得主保罗?萨缪尔森的注意。他描述当时的情景是：

诺贝尔奖得主保罗?萨缪尔森

当我打开它的时候，就好像一个全新的世界展现在我面前。

马尔可夫过程

气体分子或资产价格导致的随机运动服从马尔可夫过程，在马尔可夫过程中，未来的步骤独立于给定的历史。在极限情况下，可以证明这种随机运动趋向于通常所说的布朗运动。要理解这个概念，首先，我们需要理解布朗运动。

布朗运动背后的数学：

如果满足下列条件，则称为随机变量遵循布朗运动：

X(0)是已知的常数

随机变量X(t+h)-X(t)独立于时间t之前的过程值，具有均值uh和方差(p^2)xh的正态分布，其中u是漂移参数，p是波动率（方差的度量）。

简而言之，每一步都独立于前一步，服从正态分布。为什么悬浮在水中的花粉粒会发生布朗运动的随机运动，这一点很容易得到直观的理解，但股票价格的运动也遵循这种类型的运动，这一点却很难理解。下面是传统经济学家给出的两个理由来解释为什么股票价格应该遵循布朗运动：

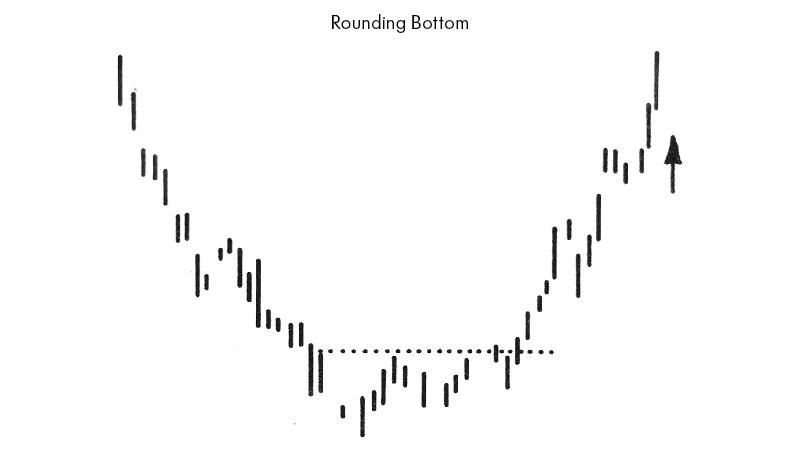1.?如果资产价格的短期变化是可预测的，那么投机者就能够通过购买低估的资产和出售高估的资产来获利。

2.?资产价格反映了所有可用的信息。因此，在一个消息灵通的市场中，资产价格会根据可获得的信息自动调整。因为如果股票价格不能反映所有可用的信息，投资者可以从中获得明确的收益，直到该信息不再对交易有用。

第二个猜想也被称为有效市场假说，由诺贝尔经济学奖得主尤金?法玛在其颇受欢迎的论文《有效资本市场：对理论和实证工作的回顾》中提出。为了把这个图像化，我们呈现了两种可视化。第一次可视化显示的是气体粒子的一维布朗运动，第二次可视化显示的是股票（初始价格为50）的布朗运动。请注意，当一个气体粒子在x轴上以+ε偏转跳跃时，同时股票价格也以+ε偏转跳跃。因此，在这种情况下，股票价格也遵循同样的布朗运动。正如所讨论的，粒子的每一步都是从一个正态分布独立于它的过去的历史。

股票价格服从布朗运动

所以，下次在投资股市之前，请记住，如果所有的投资者都是理性的，如果市场是完全知情的，那么”跑赢市场“这种说法就不会存在了。

尽管资产价格的布朗运动已经被用来推导出许多数学模型，包括布莱克-斯科尔斯公式，但一些经济学家也对其核心假设提出了批评。毕竟，人类是社会动物。我们的大多数决定都不像理性的数学定义。因此，这种非理性行为对现实市场产生了显著的影响。对这一假设持批评态度的人指出，短期内，如果股价开始上涨，继续上涨的可能性会略微增大。市场繁荣和资产泡沫就是这种非理性繁荣的例子，行为金融学经常研究这种现象。

经济碰撞的动态交换模型

想象一个由气体粒子组成的封闭容器。当初始粒子数和系统总能量均守恒时，玻尔兹曼-吉布斯分布是粒子能量最大熵值所对应的最可能分布。玻尔兹曼吉布斯分布公式如下：

上一篇：扎心了！经济学家称“上班族炒股难赚钱”，那
下一篇：没有了